DEFINICION:Una sucesión es un conjunto de términos formados según una ley o regla determinada. Por ejemplo, 1,4,9,16,25
Y 1,-x,x22- x33 ,x44,- x55 con sucesiones
Una serie es la suma indicada de los términos de una sucesión .Así, de las sucesiones anteriores obtenemos las series 1+4+9+16+25Y 1 –x + x22- x33 +x44,- x55
Cuando el numero de términos es limitado, se dice que la sucesión o serie es finita. Cuando el numero de términos es limitada, la sucesión o serie se llama una sucesión o serie infinita.
El termino general o termino enésimo es una expresión que indica la ley de formación de los términos.
EJEMPLO 1 :En la primera sucesión anterior, el termino general o termino enésimo es n2 . El primer termino se obtiene haciendo n=1, el decimo termino haciendo n=10,etc.
EJEMPLO 2 :En la segunda sucesión, el termino enésimo, con exención de n=1 ,es -xn-1n-1
Si la sucesión es infinita, se indica por puntos suspensivos, como 1,4,9…, n2
Factoriales. Una expresión que se presenta frecuentemente en el estudio de las series es el producto de números enteros sucesivos comenzando por 1.Asi, 1x 2 x3 x4 x5 es una expresión de esta clase, que se llama factoriales 5.Se entiende que n es un número y positivo


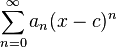
 es una serie de potencias
es una serie de potencias  es
es 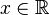
 solamente
solamente  , con
, con  , viene dado por la expresión:
, viene dado por la expresión:

 .
. .
. .
.