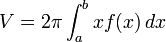Sea  una función definida en el intervalo una función definida en el intervalo ![$[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img1.gif) . .
Recibe el nombre de sólido de revolución, el sólido generado al girar alrededor del eje  , la región limitada por la gráfica de , la región limitada por la gráfica de  , el eje , el eje  y las gráficas de y las gráficas de  y y  . El eje . El eje  es un eje de simetría de dicho sólido y una sección recta perpendicular al eje es un eje de simetría de dicho sólido y una sección recta perpendicular al eje  es un círculo. es un círculo.
|
|
Para determinar el volumen de este tipo de sólidos, seguiremos un procedimiento similar al utilizado para el área de una región, aproximando el ``volumen'' de un sólido de revolución por medio de una suma de volúmenes de sólidos más elementales, en los que el volumen ya ha sido definido.
Vamos a considerar discos o cilindros circulares como los sólidos elementales, suponiendo que el volumen de un disco circular es, por definición, el producto del área

de la base por el espesor

(o altura).
Consideremos una partición

del intervalo
![$[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img1.gif)
determinada por el conjunto de números
donde

, con

.
Sea

un aumento de

.
Consideremos ahora los

discos circulares, cuyos sensores son

, y cuyas bases tienen radios

.
El volumen del

ésimo disco es:
La suma
de los volúmenes de los

discos nos da una aproximación al volumen del sólido de revolución.
Podemos suponer que mientras más delgados sean los discos, mayor será la aproximación de la suma anterior al volumen del sólido. Se tiene entonces la siguiente definición:
Si existe un número

tal que dada

exista

para la cual
para toda partición

de
![$[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img1.gif)
y todo aumento

de

, y con

, este número

es el volumen del sólido obtenido por revolución del área limitada por las gráficas de

alrededor del eje

.Si

es la función dada por
![$h(x)=\pi[f(x)]^2$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img123.gif)
para
![$x\in[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img28.gif)
, entonces la suma de aproximación:
utilizada en la definición del volumen del sólido de revolución, puede escribirse como:
donde
![$t_i\in[x_{i-1},x_i],\;\Delta x_i=x_{i-1}-x_i$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img125.gif)
.
Luego, de la definición de integral y de la definición de

dada, se tiene que
Consideremos ahora dos funciones

y

continuas en el intervalo cerrado
![$[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img1.gif)
, tales que

para
![$x\in[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img28.gif)
. Sea

la región del plano limitada por las curvas con ecuaciones

y las rectas con ecuaciones

.
Deseamos determinar el volumen

del sólido de revolución generado al girar la región

alrededor del eje

(note que en este caso
no giramos la región

alrededor de una de sus fronteras).
El sólido generado se muestra en la siguiente figura:
Sea

una partición del intervalo
![$[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img1.gif)
determinada por el conjunto de números

con

para

, y sea

un aumento de

.
En este caso, los sólidos elementales usados para obtener una suma de aproximación del volumen del sólido de revolución, serán anillos circulares.
Se muestra a continuación el

ésimo rectángulo y el

ésimo anillo circular generado al rotar aquel alrededor del eje

.
Luego, el área del anillo circular es:
por lo que el volumen del

ésimo elemento sólido será:
Entonces, la suma de aproximación para el volumen del sólido de revolución es:
Puede suponerse que mientras más delgados sean los anillos circulares, mayor será la aproximación de la suma anterior al volumen del sólido.
Si

es la función dada por
![$h=\pi\big([f(x)]^2-[g(x)]^2\big)$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img151.gif)
para
![$x\in[a,b]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img28.gif)
, entonces la suma de aproximación
utilizada en la definición 8, puede escribirse como:
donde
![$t_i\in[x_{i-1},x_i]$](http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/img153.gif)
,

.
Luego se tiene que:


![V= \pi \int_a^b ([f(x) - K]^2 - [g(x) - K]^2) \,dx](http://upload.wikimedia.org/math/4/9/3/493f2f76beba88bcf00ac729a1b90096.png)
 método de discos.
método de discos.![V= 2\pi \int_a^b (K-x)[f(x) - g(x)]\,dx](http://upload.wikimedia.org/math/8/8/7/887d1e2976691698ecb5dada988ce294.png)