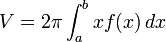lunes, 27 de junio de 2011

3.2 Longitud de Curvas

La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.
Definición:
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.
Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)2=(dx)2+(dy)2, de tal forma que sumando todos los diferenciales resulta:
Definición:
Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:

Publicado por en No hay comentarios:

lunes, 13 de junio de 2011

3.3 Cálculo de volúmenes sólidos de revolución

Los sólidos de revolución son sólidos que se generan al girar una región plana 
alrededor de un eje. Por ejemplo: el cono es un sólido que resulta al girar un 
triángulo recto alrededor  de uno de sus catetos, el cilindro surge al girar un 
rectángulo alrededor de uno de sus lados.



Se denomina sólido de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no intersecarse. Dicha recta se denomina eje de revolución.
Sea f una función continua y positiva en el intervalo [a,b]. Si la región R indicada en la figura rota alrededor del eje X, está genera un sólido de revolución cuyo volumen tratamos de determinar.

Rotaciones alrededor de los ejes cartesianos

El volumen de los sólidos generados por revolución alrededor de los ejes cartesianos se pueden obtener mediante las siguientes ecuaciones cuadráticas.


Rotación paralela al eje de abscisas (eje x)

El volumen de un sólido generado por el giro de un área comprendida entre dos gráficas, f(x) y g(x) definidas en un intervalo [a,b] alrededor de un eje horizontal, es decir, un recta paralela al eje OX de expresión y=K siendo K constante, viene dado por la siguiente fórmula genérica
V= \pi \int_a^b ([f(x) - K]^2 - [g(x) - K]^2) \,dx
En particular, si se gira una figura plana comprendida entre y=f(x), y=0, x=a y x=b alrededor del eje OX, el volumen del sólido de revolución viene generado por la fórmula:
V= \pi \int_a^b f(x)^2 \,dx método de discos.


Rotación paralela al eje de ordenadas (Eje y)

Éste es otro método que permite la obtención de volúmenes de sólidos generados por el giro de un área comprendida entre dos gráficas cualesquiera, f(x) y g(x), en un intervalo [a,b] alrededor de un eje de revolución paralelo al eje de ordenadas cuya expresión es x=K siendo K constante. La fórmula general del volumen de estos sólidos es:
V= 2\pi \int_a^b (K-x)[f(x) - g(x)]\,dx
Esta fórmula se simplifica si giramos figura plana comprendida entre y=f(x), y=0, x=a y x=b alrededor del eje OY, ya que el volumen del sólido de revolución viene generado por:
V= 2\pi \int_a^b x f(x)\,dx Método de cilindros o capas.
Publicado por en No hay comentarios:

3.4 Cálculo de centroides

Definición

Centroide es lo mismo si habláramos de Centro de Gravedad o Centro de Masa; el cual se puede ver como su punto de equilibrio, y es donde se concentras la masa de todo el cuerpo. También se puede decir que es el lugar imaginario en el que puede considerar que está concentrado todo su peso. El centroide de una figura geométrica es el centro de simetría de la misma.
Para determinar el centro de gravedad hay que tener en cuenta que toda partícula de un cuerpo situada cerca de la superficie terrestre está sometida a la acción de una fuerza, dirigida verticalmente hacia el centro de la Tierra, llamada fuerza gravitatoria.
Cuando se trata de cuerpos de dimensiones muy pequeñas frente a la Tierra, se puede admitir que las fuerzas gravitatorias que actúan sobre las distintas partículas del cuerpo son paralelas y de módulo constante. Por tanto, se puede calcular la posición del centro de gravedad hallando la recta de acción de la resultante de esas fuerzas. Si el cuerpo es homogéneo, el centro de gravedad coincide con su centro geométrico.
Si un cuerpo es tan pequeño que la aceleración de la gravedad es la misma para todas las partículas, entonces el centro de masa y el de gravedad coinciden.
En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo.
El centro de gravedad de un cuerpo no corresponde necesariamente a un punto material del cuerpo. Así, el centro de gravedad de una esfera hueca está situado en el centro de la esfera que, obviamente, no pertenece al cuerpo.
La idea al calcular el centro de gravedad de un cuerpo (bidimensional) es dividir el objeto en n partículas y sumar todas las magnitudes de los pesos de los elementos. Esto se hace para ambos ejes, x y y. Esto se puede resumir con las siguientes fórmulas:
W=∫dW   (peso)             x W=∫x dW               yW=∫y dW

Método de cálculo

En primer lugar se debe identificar la figura a la cual se le buscara el centroide.
En segundo lugar es de ver si la figura consta de formas geométricas definidas.
Después se le sacara el área a cada forma geométrica encontrada. (En este caso se ocuparan las fórmulas de área del cuadrado, rectángulo, triangulo, circulo, etc…)
Después se debe ocupar las ecuaciones para encontrar el centroide en XC y en YC cuyas formulas son:

XC= (A1*X1)+(A2*X2)+…/ A1+A2+….

YC= (A1*Y1)+(A2*Y2)+…/ A1+A2+….

Bueno las X1, X2, Y1, Y2 van a depender de la forma geométrica de cada área encontrada, porque cada forma geométrica tiene su fórmula.

EJEMPLO DE COMO ENCONTRAR EL CENTROIDE.

1) Establecemos los ejes.
2) Como segundo paso dividimos la figura en áreas más simples de centroide conocidas y trabajamos con la más sencilla.
3) Luego vamos a buscar el eje “Y” centroidal, es decir el eje paralelo al eje “Y” de referencia, asumiendo que cada área es la carga y la distancia x de sus centroides su brazo.
4) Hacemos lo mismo para encontrar el eje centroidal “X” haciendo momento de las áreas respecto al eje “X” de referencia.
5) Ya tenemos el centroide de la figura y sus ejes centroidales. En ocasiones como esta, puede estar ubicado fuera de la figura.


Publicado por en 1 comentario:

jueves, 9 de junio de 2011

3.5 Otras Aplicaciones

Sea $f$ una función definida en el intervalo $[a,b]$.
Recibe el nombre de sólido de revolución, el sólido generado al girar alrededor del eje $x$, la región limitada por la gráfica de $y=f(x)$, el eje $x$ y las gráficas de $x=a$ y $x=b$. El eje $x$ es un eje de simetría de dicho sólido y una sección recta perpendicular al eje $x$ es un círculo.


Para determinar el volumen de este tipo de sólidos, seguiremos un procedimiento similar al utilizado para el área de una región, aproximando el ``volumen'' de un sólido de revolución por medio de una suma de volúmenes de sólidos más elementales, en los que el volumen ya ha sido definido.
Vamos a considerar discos o cilindros circulares como los sólidos elementales, suponiendo que el volumen de un disco circular es, por definición, el producto del área $A$ de la base por el espesor $d$ (o altura).

Consideremos una partición $P_n$ del intervalo $[a,b]$ determinada por el conjunto de números
\begin{displaymath}\{ x_0,x_1,x_2,\dots,x_{i-1},x_i,\dots,x_{n-1},x_n \},\end{displaymath}

donde $\Delta x_i=x_{i-1}-x_i$, con $i\in\{1,2,3,\dots,n\}$.
Sea $T_n=\{t_1,t_2,\dots,t_n\}$ un aumento de $P_n$.
Consideremos ahora los $n$ discos circulares, cuyos sensores son$\Delta x_1,\Delta x_2,\dots,\Delta x_i,\dots,\Delta x_n$, y cuyas bases tienen radios$f(t_1),f(t_2),\dots,f(t_i),\dots,f(t_n)$.


El volumen del $i-$ésimo disco es:
\begin{displaymath}\pi[f(t_i)]^2\cdot\Delta x_i\end{displaymath}
 La suma
\begin{displaymath}\sum_{i=1}^n\pi[f(t_i)]^2\cdot\Delta x_i\end{displaymath}

de los volúmenes de los $n$ discos nos da una aproximación al volumen del sólido de revolución.
Podemos suponer que mientras más delgados sean los discos, mayor será la aproximación de la suma anterior al volumen del sólido. Se tiene entonces la siguiente definición:


Si existe un número $V$ tal que dada $\epsilon>0$ exista $\delta>0$ para la cual

\begin{displaymath}\left\vert\sum_{i=1}^n\pi[f(t_i)]^2\cdot\Delta x_i-V\right\vert<\epsilon\end{displaymath}


para toda partición $P_n$ de $[a,b]$ y todo aumento $T_n$ de $P_n$, y con $N_p<\delta$, este número $V$ es el volumen del sólido obtenido por revolución del área limitada por las gráficas de $y=f(x),\;y=0,\;x=a,\;x=b$ alrededor del eje $x$.Si $h$ es la función dada por $h(x)=\pi[f(x)]^2$ para $x\in[a,b]$, entonces la suma de aproximación:
\begin{displaymath}\sum_{i=1}^n\pi[f(t_i)]^2\cdot\Delta x_i\end{displaymath}

utilizada en la definición del volumen del sólido de revolución, puede escribirse como:
\begin{displaymath}\sum_{i=1}^nh(t_i)\cdot\Delta x_i\end{displaymath}

donde $t_i\in[x_{i-1},x_i],\;\Delta x_i=x_{i-1}-x_i$.
Luego, de la definición de integral y de la definición de $V$ dada, se tiene que

\begin{displaymath}\displaystyle V=\int_a^bh(x)\,dx=\int_a^b\pi[f(x)]^2\,dx\end{displaymath}
 
 
 Consideremos ahora dos funciones $f$ y $g$ continuas en el intervalo cerrado $[a,b]$, tales que $f(x)\geq g(x)$ para $x\in[a,b]$. Sea $R$ la región del plano limitada por las curvas con ecuaciones $y=f(x),\;y=g(x)$ y las rectas con ecuaciones $x=a,\;x=b$.

Deseamos determinar el volumen $V$ del sólido de revolución generado al girar la región $R$ alrededor del eje $x$ (note que en este caso no giramos la región $R$alrededor de una de sus fronteras).
El sólido generado se muestra en la siguiente figura:



Sea $P_n$ una partición del intervalo $[a,b]$ determinada por el conjunto de números$\{x_0,x_1,x_2,\dots,x_{i-1},x_i,\dots,x_n\}$ con $\Delta x_i=x_i-x_{i-1}$ para $i\in\{1,2,\dots,n\}$, y sea$T_n=\{t_1,t_2,\dots,t_i,\dots,t_n\}$ un aumento de $P_n$.
En este caso, los sólidos elementales usados para obtener una suma de aproximación del volumen del sólido de revolución, serán anillos circulares.
Se muestra a continuación el $i-$ésimo rectángulo y el $i-$ésimo anillo circular generado al rotar aquel alrededor del eje $x$.



Luego, el área del anillo circular es:
\begin{displaymath}\pi[f(t_i)]^2-\pi[g(t_i)]^2\end{displaymath}

por lo que el volumen del $i-$ésimo elemento sólido será:
\begin{displaymath}\Delta V_i=\pi\big([f(t_i)]^2-[g(t_i)]^2\big)\cdot\Delta x_i\end{displaymath}

Entonces, la suma de aproximación para el volumen del sólido de revolución es:
\begin{displaymath}\sum_{i=1}^n\pi\big([f(t_i)]^2-[g(t_i)]^2\big)\cdot\Delta x_i\end{displaymath}

Puede suponerse que mientras más delgados sean los anillos circulares, mayor será la aproximación de la suma anterior al volumen del sólido.

 Definición
 Si existe un número $V$ tal que dada $\epsilon>0$ exista $\delta>0$ para la cual

\begin{displaymath}\displaystyle \left\vert\sum_{i=1}^n\pi\big([f(t_i)]^2-[g(t_i)]^2\big)\Delta x_i-V\right\vert<\epsilon\end{displaymath}
 
 para toda partición $P_n$ de $[a,b]$ y todo aumento $T_n$ de $P_n$, y con $N_p<\delta$, este número de $V$ es el volumen del sólido obtenido por revolución del área limitada por las gráficas de $y=f(x)$, $y=g(x)$, $x=a$, $x=b$, alrededor del eje $x$.

Si $h$ es la función dada por $h=\pi\big([f(x)]^2-[g(x)]^2\big)$ para $x\in[a,b]$, entonces la suma de aproximación
\begin{displaymath}\sum_{i=1}^n\pi\big([f(t_i)]^2-[g(t_i)]^2\big)\cdot\Delta x_i\end{displaymath}
 utilizada en la definición 8, puede escribirse como:
\begin{displaymath}\displaystyle \sum_{i=1}^nh(t_i)\,\Delta x_i\end{displaymath}

donde $t_i\in[x_{i-1},x_i]$, $\Delta x_i=x_i-x_{i-1}$.
Luego se tiene que:
\begin{displaymath}V=\displaystyle \int_a^bh(x)\,dx=\int_a^b\pi\big([f(x)]^2-[g(x)]^2\big)\,dx\end{displaymath}
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)